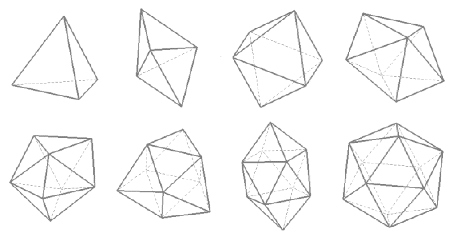
À la découverte des deltaèdres, de la relation entre les nombres de sommets, arêtes et faces, des deltaèdres convexes.
Activité 1 : faces, sommets, arêtes, à la découverte des deltaèdres
-Chercher tous les deltaèdres possédant un certain nombre de faces.
-Commencer avec 4 faces.
-Pour chacun des modèles trouvés, remplir le tableau.
| Nombre de sommets | ___ | ___ | ___ | ___ | ___ | ___ | ___ | ___ | ___ | ___ | ___ | ___ |
| Nombre d’arêtes | ___ | ___ | ___ | ___ | ___ | ___ | ___ | ___ | ___ | ___ | ___ | ___ |
| Nombre de faces | ___ | ___ | ___ | ___ | ___ | ___ | ___ | ___ | ___ | ___ | ___ | ___ |
-Utiliser le tableau pour trouver un certain nombre de propriétés concernant les nombres de faces, d’arêtes et de sommets.
- Par exemple, est-ce qu’on peut fabriquer un deltaèdre comportant n’importe quel nombre de faces, n’importe quel nombre de sommets, n’importe quel nombre d’arêtes ?
- Est-ce qu’il y a beaucoup de deltaèdres à 4 faces, à 6 faces, à 8 faces, à 10 faces, voire à 12 faces ?
Activité 2 : les deltaèdres convexes
Un deltaèdre convexe est un deltaèdre qui n’a pas de creux.
– Fabriquer un sommet de 6 faces. Est-ce qu’un deltaèdre convexe peut avoir un sommet de 6 faces ?
– Fabriquer un sommet de 7 faces. Qu’en pensez vous.
– Faire sentir à l’aide d’un découpage que la somme des angles d’un sommet ne peut pas atteindre ou dépasser 360 degrés.
– Chercher à fabriquer tous les deltaèdres convexes possibles. Pour chacun, remplir le tableau. Est-ce que le tableau présente des trous ? Est-ce qu’il s’arrête ?
– Construire de beaux modèles de ces deltaèdres converxes, par divers moyens.
– (Eventuellement) Rechercher des documents sur internet sur les deltaèdres convexes
Activité 3 : les patrons de deltaèdres
1. Une figure plane d’une seule pièce composée d’un nombre fini de triangles équilatéraux adjacents et sans trous s’appelle un polyamant.
L’activité consiste à fabriquer par exemple tous les polyamants avec 4 triangles, ou plus, et chercher ceux qui sont des patrons de deltaèdres.
– Y a-t-il des polyamants qui sont les patrons de plusieurs deltaèdres distincts ?
– Se donner un deltaèdre. Combien a-t-il de patrons distincts ; est-ce que tous les deltaèdres ont des patrons ?
– Découper les polyamants dans du papier préparé à cet effet, et les classer par nombre de triangles, en séparant ceux qui sont des patrons de deltaèdres et ceux qui n’en sont pas.
2. Il y a des polyamants avec lesquels on ne peut pas paver le plan. En trouver un. Essayer d’en trouver qui aient le moins de triangles possibles.
Quelques résultats utiles
Formule d’Euler pour un polyèdre « sans trou », qu’il soit convexe ou non :
s-a+f=2
où
– s est le nombre de sommets
– a est le nombre d’arêtes
– f est le nombre de faces
Le nombre de faces d’un deltaèdre est toujours pair. Il commence à 4.
Le nombre d’arêtes est un mutiple de 3. Il commence à 6 ; celui des sommets commence à 4 et augmente de un en un.
| s | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| a | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| f | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
Il n’y a qu’un seul deltaèdre à 4 faces, un seul à 6 et un seul à 8 faces. Pour 10 faces, il y en a cinq, mais l’un d’eux a en fait des faces coplanaires formant un losange, ce qui n’en fait plus un « vrai » deltaèdre.
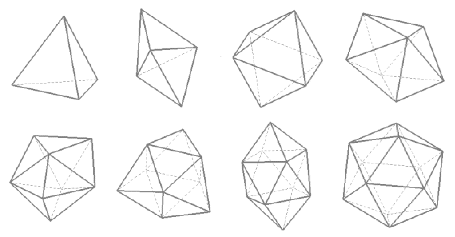
Il n’existe que 8 deltaèdres convexes, avec des nombres de faces égaux à 4, 6, 8, 10, 12, 14, 16, 20.
Récréations
On peut construire beaucoup d’autres choses avec des triangles équilatéraux. On peut laisser les enfants explorer des formes possibles (polyèdres étoilés…) ou leur en suggérer, et leur faire construire ensuite ces formes avec divers matériaux (pailles, carton, etc.).
Parmi les formes que l’on peut explorer : des fractales, des pavages (exemple : le sphinx).
On peut essayer de tresser un oicosaèdre : c’est difficile mais le résultat est très joli et on peut en faire des assemblages.
En savoir plus…
Un document plus complet sur les deltaèdres, comportant notamment des démonstrations de relations :
Les deltaèdres